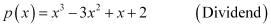Question 1:
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) 
Quotient = x − 3
Remainder = 7x − 9
Quotient = x2 + x − 3
Remainder = 8
Quotient = −x2 − 2
Remainder = −5x +10
Question 2:
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
= Since the remainder is 0,
Hence,
Since the remainder is 0,
Hence,
Since the remainder
is not a factor of
Question 3:
Obtain all other zeroes of ,
if two of its zeroes are .
if two of its zeroes are .
We factorize
Therefore, its zero is given by x + 1 = 0
x = −1
As it has the term ,
therefore, there will be 2 zeroes at x = −1.
Hence, the zeroes of the given polynomial are,
Question 4:
On dividing
by a polynomial g(x), the quotient and remainder were x − 2 and − 2x + 4, respectively. Find g(x).
by a polynomial g(x), the quotient and remainder were x − 2 and − 2x + 4, respectively. Find g(x).
g(x) = ? (Divisor)
Quotient = (x − 2)
Remainder = (− 2x + 4)
Dividend = Divisor × Quotient + Remainder
g(x) is the quotient when we divide
Question 5:
Give examples of polynomial p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
According to the division algorithm, if p(x) and g(x) are two polynomials with
g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that
p(x) = g(x) × q(x) + r(x),
where r(x) = 0 or degree of r(x) < degree of g(x)
Degree of a polynomial is the highest power of the variable in the polynomial.
(i) deg p(x) = deg q(x)
Degree of quotient will be equal to degree of dividend when divisor is constant ( i.e., when any polynomial is divided by a constant).
Let us assume the division of
by 2.
Here, p(x) =
g(x) = 2
q(x) =
and r(x) = 0
Degree of p(x) and q(x) is the same i.e., 2.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
= 2()
=
Thus, the division algorithm is satisfied.
(ii) deg q(x) = deg r(x)
Let us assume the division of x3 + x by x2,
Here, p(x) = x3 + x
g(x) = x2
q(x) = x and r(x) = x
Clearly, the degree of q(x) and r(x) is the same i.e., 1.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
x3 + x = (x2 ) × x + x
x3 + x = x3 + x
Thus, the division algorithm is satisfied.
(iii)deg r(x) = 0
Degree of remainder will be 0 when remainder comes to a constant.
Let us assume the division of x3 + 1by x2.
Here, p(x) = x3 + 1
g(x) = x2
q(x) = x and r(x) = 1
Clearly, the degree of r(x) is 0.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
x3 + 1 = (x2 ) × x + 1
x3 + 1 = x3 + 1
Thus, the division algorithm is satisfied.
g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that
p(x) = g(x) × q(x) + r(x),
where r(x) = 0 or degree of r(x) < degree of g(x)
Degree of a polynomial is the highest power of the variable in the polynomial.
(i) deg p(x) = deg q(x)
Degree of quotient will be equal to degree of dividend when divisor is constant ( i.e., when any polynomial is divided by a constant).
Let us assume the division of
by 2.Here, p(x) =
g(x) = 2
q(x) =
and r(x) = 0Degree of p(x) and q(x) is the same i.e., 2.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
= 2()=
Thus, the division algorithm is satisfied.
(ii) deg q(x) = deg r(x)
Let us assume the division of x3 + x by x2,
Here, p(x) = x3 + x
g(x) = x2
q(x) = x and r(x) = x
Clearly, the degree of q(x) and r(x) is the same i.e., 1.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
x3 + x = (x2 ) × x + x
x3 + x = x3 + x
Thus, the division algorithm is satisfied.
(iii)deg r(x) = 0
Degree of remainder will be 0 when remainder comes to a constant.
Let us assume the division of x3 + 1by x2.
Here, p(x) = x3 + 1
g(x) = x2
q(x) = x and r(x) = 1
Clearly, the degree of r(x) is 0.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
x3 + 1 = (x2 ) × x + 1
x3 + 1 = x3 + 1
Thus, the division algorithm is satisfied.