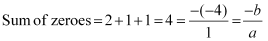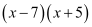Question 1:
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i)
Therefore,
, 1, and −2 are the zeroes of the given polynomial.
Comparing the given polynomial with ,
we obtain a = 2, b = 1, c = −5, d = 2
Therefore, the relationship between the zeroes and the coefficients is verified.
(ii)
Therefore, 2, 1, 1 are the zeroes of the given polynomial.
Comparing the given polynomial with ,
we obtain a = 1, b = −4, c = 5, d = −2.
Verification of the relationship between zeroes and coefficient of the given polynomial
Multiplication of zeroes taking two at a time = (2)(1) + (1)(1) + (2)(1) =2 + 1 + 2 = 5
Multiplication of zeroes = 2 × 1 × 1 = 2
Hence, the relationship between the zeroes and the coefficients is verified.
Question 2:
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, − 7, − 14 respectively.
Let the polynomial be
and the zeroes be
.
It is given that
If a = 1, then b = −2, c = −7, d = 14
Hence, the polynomial is
.
and the zeroes be
It is given that
If a = 1, then b = −2, c = −7, d = 14
Hence, the polynomial is
Question 3:
If the zeroes of polynomial
are,
find a and b.
are,
find a and b.
Zeroes are a − b, a + a + b
Comparing the given polynomial with ,
we obtain
p = 1, q = −3, r = 1, t = 1
The zeroes are .
Hence, a = 1 and b =
.
Question 4:
If two zeroes of the polynomial
are,
find other zeroes.
are,
find other zeroes.
Given that 2 +
and 2-
are zeroes of the given polynomial.
Therefore
= x2 + 4 − 4x − 3
= x2 − 4x + 1 is a factor of the given polynomial
For finding the remaining zeroes of the given polynomial, we will find the quotient by dividing
by x2 − 4x + 1.
Clearly,
=
It can be observed that
is also a factor of the given polynomial.
And
=
Therefore, the value of the polynomial is also zero when
or
Or x = 7 or −5
Hence, 7 and −5 are also zeroes of this polynomial.
Question 5:
Therefore
= x2 + 4 − 4x − 3= x2 − 4x + 1 is a factor of the given polynomial
For finding the remaining zeroes of the given polynomial, we will find the quotient by dividing
by x2 − 4x + 1.
Clearly,
It can be observed that
And
Hence, 7 and −5 are also zeroes of this polynomial.
Question 5:
If the polynomial
is divided by another polynomial
,
the remainder comes out to be x + a, find k and a.
is divided by another polynomial
the remainder comes out to be x + a, find k and a.
By division algorithm,
Dividend = Divisor × Quotient + Remainder
Dividend − Remainder = Divisor × Quotient
will be perfectly divisible by
.
Let us divide
by
It can be observed that
will be 0.
Therefore,
= 0 and
= 0
For
= 0,
2 k =10
And thus, k = 5
For
= 0
10 − a − 8 × 5 + 25 = 0
10 − a − 40 + 25 = 0
− 5 − a = 0
Therefore, a = −5
Hence, k = 5 and a = −5
Dividend = Divisor × Quotient + Remainder
Dividend − Remainder = Divisor × Quotient
.
Therefore,
For
2 k =10
And thus, k = 5
For
10 − a − 8 × 5 + 25 = 0
10 − a − 40 + 25 = 0
− 5 − a = 0
Therefore, a = −5
Hence, k = 5 and a = −5