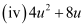Question 1:
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
The value of
is zero when x − 4 = 0 or x + 2 = 0, i.e., when x = 4 or x = −2Therefore, the zeroes of
are 4 and −2.Sum of zeroes =
Product of zeroes
The value of 4s2 − 4s + 1 is zero when 2s − 1 = 0, i.e.
,Therefore, the zeroes of 4s2 − 4s + 1 are
and .Sum of zeroes =
Product of zeroes
The value of 6x2 − 3 − 7x is zero when 3x + 1 = 0 or 2x − 3 = 0, i.e.,
or 
Therefore, the zeroes of 6x2 − 3 − 7x are
.Sum of zeroes =
Product of zeroes =
Question 2:
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
