Exercise 8.4

Question 1:

Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.

We know that,

will always be positive as we are adding two positive quantities.
Therefore,

We know that,

However,

Therefore,

Also,

Question 2:

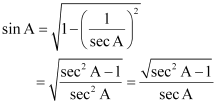
Write all the other trigonometric ratios of ∠A in terms of sec A.

We know that,

Also, sin² A + cos² A = 1
sin² A = 1 − cos² A

tan²A + 1 = sec²A
tan²A = sec²A − 1

Question 3:

Evaluate

(i)

(ii) sin25° cos65° + cos25° sin65°

(i)

(As sin²A + cos²A = 1)
= 1
(ii) sin25° cos65° + cos25° sin65°

= sin²25° + cos²25°
= 1 (As sin²A + cos²A = 1)

Question 4:

Choose the correct option. Justify your choice.

(i) 9 sec² A − 9 tan² A =

(A) 1

(B) 9

(C) 8

(D) 0

(ii) (1 + tan θ + sec θ) (1 + cot θ − cosec θ)

(A) 0

(B) 1

(C) 2

(D) −1

(iii) (secA + tanA) (1 − sinA) =

(A) secA

(B) sinA

(C) cosecA

(D) cosA

(iv)

(A) sec² A

(B) −1

(C) cot² A

(D) tan² A

(i) 9 sec²A − 9 tan²A
= 9 (sec²A − tan²A)
= 9 (1) [As sec² A − tan² A = 1]
= 9
Hence, alternative (B) is correct.
(ii)
(1 + tan θ + sec θ) (1 + cot θ − cosec θ)

Hence, alternative (C) is correct.
(iii) (secA + tanA) (1 − sinA)

 

= cosA
Hence, alternative (D) is correct.
(iv)

 

Hence, alternative (D) is correct.