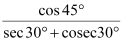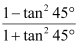CBSE Class X: Exercise 8.2

Question 1:

Evaluate the following

(i) sin60° cos30° + sin30° cos 60°

(ii) 2tan²45° + cos²30° − sin²60°

(iii)

(iv)

(v)

(i) sin60° cos30° + sin30° cos 60°

(ii) 2tan²45° + cos²30° − sin²60°

(iii)

(iv)

(v)

Question 2:

Choose the correct option and justify your choice.

(i)

(A). sin60°

(B). cos60°

(C). tan60°

(D). sin30°

(ii)

(A). tan90°

(B). 1

(C). sin45°

(D). 0

(iii) sin2A = 2sinA is true when A =

(A). 0°

(B). 30°

(C). 45°

(D). 60°

(iv)

(A). cos60°

(B). sin60°

(C). tan60°

(D). sin30°

(i)

Out of the given alternatives, only

Hence, (A) is correct.
(ii)

Hence, (D) is correct.
(iii)Out of the given alternatives, only A = 0° is correct.
As sin 2A = sin 0° = 0
2 sinA = 2sin 0° = 2(0) = 0
Hence, (A) is correct.
(iv)

Out of the given alternatives, only tan 60°

Hence, (C) is correct.

Question 3:

and;

0° < A + B ≤ 90°, A > B find A and B.

⇒

⇒ A + B = 60 … (1)

⇒ tan (A − B) = tan30
⇒ A − B = 30 … (2)
On adding both equations, we obtain
2A = 90
⇒ A = 45
From equation (1), we obtain
45 + B = 60
B = 15
Therefore, ∠A = 45° and ∠B = 15°

Question 4:

State whether the following are true or false. Justify your answer.

(i) sin (A + B) = sin A + sin B

(ii) The value of sinθ increases as θ increases

(iii) The value of cos θ increases as θ increases

(iv) sinθ = cos θ for all values of θ

(v) cot A is not defined for A = 0°

(i) sin (A + B) = sin A + sin B
Let A = 30° and B = 60°
sin (A + B) = sin (30° + 60°)
= sin 90°
= 1
sin A + sin B = sin 30° + sin 60°

Clearly, sin (A + B) ≠ sin A + sin B
Hence, the given statement is false.
(ii) The value of sin θ increases as θ increases in the interval of 0° < θ < 90° as
sin 0° = 0

sin 90° = 1
Hence, the given statement is true.
(iii) cos 0° = 1

cos90° = 0
It can be observed that the value of cos θ does not increase in the interval of 0° < θ < 90°.
Hence, the given statement is false.
(iv) sin θ = cos θ for all values of θ.
This is true when θ = 45°
As