Exercise 6.2

Question 1:

In figure.6.17. (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

(i)

(ii)

(i)

Let EC = x cm
It is given that DE || BC.
By using basic proportionality theorem, we obtain

(ii)

Let AD = x cm
It is given that DE || BC.
By using basic proportionality theorem, we obtain

     

Question 2:

E and F are points on the sides PQ and PR respectively of a ΔPQR. For each of the following cases, state whether EF || QR.

(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

(iii)PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.63 cm 

(i)

Given that, PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm, FR = 2.4 cm

(ii)

PE = 4 cm, QE = 4.5 cm, PF = 8 cm, RF = 9 cm

(iii)

PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, PF = 0.36 cm

Question 3:

In the following figure, if LM || CB and LN || CD, prove that 


 AM/AB---AN/AD

In the given figure, LM || CB
By using basic proportionality theorem, we obtain

Question 4:

In the following figure, DE || AC and DF || AE. Prove that 

In ΔABC, DE || AC

Question 5:

In the following figure, DE || OQ and DF || OR, show that EF || QR. 

In Δ POQ, DE || OQ

Question 6:

In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

In Δ POQ, AB || PQ

Question 7:

Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).

Consider the given figure in which PQ is a line segment drawn through the mid-point P of line AB, such that

 

Or, Q is the mid-point of AC.

Question 8:

Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).

Consider the given figure in which PQ is a line segment joining the mid-points P and Q of line AB and AC respectively.
i.e., AP = PB and AQ = QC
It can be observed that

Hence, by using basic proportionality theorem, we obtain

Question 9:

ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that

Draw a line EF through point O, such that

In ΔADC,

By using basic proportionality theorem, we obtain

In ΔABD,

So, by using basic proportionality theorem, we obtain

From equations (1) and (2), we obtain

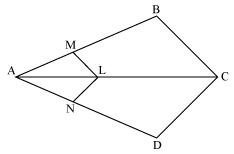
Question 10:

The diagonals of a quadrilateral ABCD intersect each other at the point O such that 

 Show that ABCD is a trapezium.

Let us consider the following figure for the given question

Draw a line OE || AB

In ΔABD, OE || AB
By using basic proportionality theorem, we obtain

However, it is given that

⇒ EO || DC [By the converse of basic proportionality theorem]
⇒ AB || OE || DC

 ⇒ AB || CD
∴ ABCD is a trapezium.