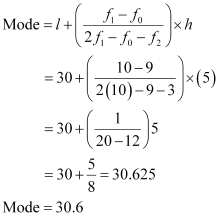Exercise 14.2

Question 1:

The following table shows the ages of the patients admitted in a hospital during a year:

age (in years)	5 − 15	15 − 25	25 − 35	35 − 45	45 − 55	55 − 65
Number of patients	6	11	21	23	14	5

Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency. 

To find the class marks (x_i), the following relation is used.

Taking 30 as assumed mean (a), d_i and f_id_iare calculated as follows.

Age (in years)	Number of patients fi	Class mark xi	di = xi − 30	fidi
5 − 15	6	10	− 20	− 120
15 − 25	11	20	− 10	− 110
25 − 35	21	30	0	0
35 − 45	23	40	10	230
45 − 55	14	50	20	280
55 − 65	5	60	30	150
Total	80			430

From the table, we obtain

Mean of this data is 35.38. It represents that on an average, the age of a patient admitted to hospital was 35.38 years.
It can be observed that the maximum class frequency is 23 belonging to class interval 35 − 45.
Modal class = 35 − 45
Lower limit (l) of modal class = 35
Frequency (f₁) of modal class = 23
Class size (h) = 10
Frequency (f₀) of class preceding the modal class = 21
Frequency (f₂) of class succeeding the modal class = 14
Mode =

Mode is 36.8. It represents that the age of maximum number of patients admitted in hospital was 36.8 years.

Question 2:

The following data gives the information on the observed lifetimes (in hours) of 225 electrical components:

Lifetimes (in hours)	0 − 20	20 − 40	40 − 60	60 − 80	80 − 100	100 − 120
Frequency	10	35	52	61	38	29

Determine the modal lifetimes of the components. 

From the data given above, it can be observed that the maximum class frequency is 61, belonging to class interval 60 − 80.
Therefore, modal class = 60 − 80
Lower class limit (l) of modal class = 60
Frequency (f₁) of modal class = 61
Frequency (f₀) of class preceding the modal class = 52
Frequency (f₂) of class succeeding the modal class = 38
Class size (h) = 20

Therefore, modal lifetime of electrical components is 65.625 hours.

Question 3:

The following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure.

Expenditure (in Rs)	Number of families
1000 − 1500	24
1500 − 2000	40
2000 − 2500	33
2500 − 3000	28
3000 − 3500	30
3500 − 4000	22
4000 − 4500	16
4500 − 5000	7

It can be observed from the given data that the maximum class frequency is 40, belonging to 1500 − 2000 intervals.
Therefore, modal class = 1500 − 2000
Lower limit (l) of modal class = 1500
Frequency (f₁) of modal class = 40
Frequency (f₀) of class preceding modal class = 24
Frequency (f₂) of class succeeding modal class = 33
Class size (h) = 500

Therefore, modal monthly expenditure was Rs 1847.83.
To find the class mark, the following relation is used.

Class size (h) of the given data = 500
Taking 2750 as assumed mean (a), d_i, u_i, and f_iu_iare calculated as follows.

Expenditure (in Rs)	Number of families fi	xi	di = xi − 2750		fiui
1000 − 1500	24	1250	− 1500	− 3	− 72
1500 − 2000	40	1750	− 1000	− 2	− 80
2000 − 2500	33	2250	− 500	− 1	− 33
2500 − 3000	28	2750	0	0	0
3000 − 3500	30	3250	500	1	30
3500 − 4000	22	3750	1000	2	44
4000 − 4500	16	4250	1500	3	48
4500 − 5000	7	4750	2000	4	28
Total	200				− 35

From the table, we obtain

Therefore, mean monthly expenditure was Rs 2662.50.

Question 4:

The following distribution gives the state-wise teacher-student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret the two measures.

Number of students per teacher	Number of states/U.T
15 − 20	3
20 − 25	8
25 − 30	9
30 − 35	10
35 − 40	3
40 − 45	0
45 − 50	0
50 − 55	2

It can be observed from the given data that the maximum class frequency is 10 belonging to class interval 30 − 35.
Therefore, modal class = 30 − 35
Class size (h) = 5
Lower limit (l) of modal class = 30
Frequency (f₁) of modal class = 10
Frequency (f₀) of class preceding modal class = 9
Frequency (f₂) of class succeeding modal class = 3

It represents that most of the states/U.T have a teacher-student ratio as 30.6.
To find the class marks, the following relation is used.

Taking 32.5 as assumed mean (a), d_i, u_i, and f_iu_i are calculated as follows.

Number of students per teacher	Number of states/U.T (fi)	xi	di = xi − 32.5		fiui
15 − 20	3	17.5	− 15	− 3	− 9
20 − 25	8	22.5	− 10	− 2	− 16
25 − 30	9	27.5	− 5	− 1	− 9
30 − 35	10	32.5	0	0	0
35 − 40	3	37.5	5	1	3
40 − 45	0	42.5	10	2	0
45 − 50	0	47.5	15	3	0
50 − 55	2	52.5	20	4	8
Total	35				− 23

Therefore, mean of the data is 29.2.
It represents that on an average, teacher−student ratio was 29.2.

Question 5:

The given distribution shows the number of runs scored by some top batsmen of the world in one-day international cricket matches.

Runs scored	Number of batsmen
3000 − 4000	4
4000 − 5000	18
5000 − 6000	9
6000 − 7000	7
7000 − 8000	6
8000 − 9000	3
9000 − 10000	1
10000 − 11000	1

Find the mode of the data.

From the given data, it can be observed that the maximum class frequency is 18, belonging to class interval 4000 − 5000.
Therefore, modal class = 4000 − 5000
Lower limit (l) of modal class = 4000
Frequency (f₁) of modal class = 18
Frequency (f₀) of class preceding modal class = 4
Frequency (f₂) of class succeeding modal class = 9
Class size (h) = 1000

Therefore, mode of the given data is 4608.7 runs.

Question 6:

A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarised it in the table given below. Find the mode of the data:

Number of cars	0 − 10	10 − 20	20 − 30	30 − 40	40 − 50	50 − 60	60 − 70	70 − 80
Frequency	7	14	13	12	20	11	15	8

From the given data, it can be observed that the maximum class frequency is 20, belonging to 40 − 50 class intervals.
Therefore, modal class = 40 − 50
Lower limit (l) of modal class = 40
Frequency (f₁) of modal class = 20
Frequency (f₀) of class preceding modal class = 12
Frequency (f₂) of class succeeding modal class = 11
Class size = 10

Therefore, mode of this data is 44.7 cars.