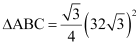Question 1:
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
It can be observed that RQ is the diameter of the circle. Therefore, ∠RPQ will be 90º.
By applying Pythagoras theorem in ΔPQR,
RP2 + PQ2 = RQ2
(7)2 + (24)2 = RQ2
Radius of circle,
Area of PQR=
Area pf shaded region=Area of semi circleRPQOR- Area of PQR
Question 2:
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.
Radius of inner circle = 7 cm
Radius of outer circle = 14 cm
Area of shaded region = Area of sector OAFC − Area of sector OBED
Question 3:
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
It can be observed from the figure that the radius of each semi-circle is 7 cm.
Area of each semi-circle =
Area of square ABCD = (Side)2 = (14)2 = 196 cm2
Area of the shaded region
= Area of square ABCD − Area of semi-circle APD − Area of semi-circle BPC
= 196 − 77 − 77 = 196 − 154 = 42 cm2
Area of each semi-circle =
Area of square ABCD = (Side)2 = (14)2 = 196 cm2
Area of the shaded region
= Area of square ABCD − Area of semi-circle APD − Area of semi-circle BPC
= 196 − 77 − 77 = 196 − 154 = 42 cm2
Question 4:
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
We know that each interior angle of an equilateral triangle is of measure 60°.
Area of sector OCDE
Area of
Area of circle = πr2
Area of shaded region = Area of ΔOAB + Area of circle − Area of sector OCDE
Each quadrant is a sector of 90° in a circle of 1 cm radius.
Area of each quadrant
Area of square = (Side)2 = (4)2 = 16 cm2
Area of circle = πr2 = π (1)2
Area of the shaded region = Area of square − Area of circle − 4 × Area of quadrant
Radius (r) of circle = 32 cm
AD is the median of
ABC.
AD = 48 cm
In ΔABD,
AB2 = AD2 + BD2
Area of equilateral triangle,
Area of circle = πr2
Area of design = Area of circle − Area of ΔABC
Area of each of the 4 sectors is equal to each other and is a sector of 90° in a circle of 7 cm radius.
Area of each sector
Area of square ABCD = (Side)2 = (14)2 = 196 cm2
Area of shaded portion = Area of square ABCD − 4 × Area of each sector
Therefore, the area of shaded portion is 42 cm2.
Distance around the track along its inner edge = AB + arc BEC + CD + arc DFA
Area of the track = (Area of GHIJ − Area of ABCD) + (Area of semi-circle HKI − Area of semi-circle BEC) + (Area of semi-circle GLJ − Area of semi-circle AFD)
Therefore, the area of the track is 4320 m2.
Radius (r1) of larger circle = 7 cm
Radius (r2) of smaller circle
Area of smaller circle
Area of semi-circle AECFB of larger circle
Area of
Area of the shaded region
= Area of smaller circle + Area of semi-circle AECFB − Area of ΔABC
Let the side of the equilateral triangle be a.
Area of equilateral triangle = 17320.5 cm2
Each sector is of measure 60°.
Area of sector ADEF
Area of shaded region = Area of equilateral triangle − 3 × Area of each sector
From the figure, it can be observed that the side of the square is 42 cm.
Area of square = (Side)2 = (42)2 = 1764 cm2
Area of each circle = πr2
Area of 9 circles = 9 × 154 = 1386 cm2
Area of the remaining portion of the handkerchief = 1764 − 1386 = 378 cm2
(i) Since OACB is a quadrant, it will subtend 90° angle at O.
Area of quadrant OACB
(ii) Area of ΔOBD
Area of the shaded region = Area of quadrant OACB − Area of ΔOBD
In ΔOAB,
OB2 = OA2 + AB2
= (20)2 + (20)2
Radius (r) of circle
Area of quadrant OPBQ
Area of OABC = (Side)2 = (20)2 = 400 cm2
Area of shaded region = Area of quadrant OPBQ − Area of OABC
= (628 − 400) cm2
= 228 cm2
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region.
Area of the shaded region = Area of sector OAEB − Area of sector OCFD
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
As ABC is a quadrant of the circle, ∠BAC will be of measure 90º.
In ΔABC,
BC2 = AC2 + AB2
= (14)2 + (14)2
Radius (r1) of semi-circle drawn on
Area of
Area of sector
= 154 − (154 − 98)
= 98 cm2
The designed area is the common region between two sectors BAEC and DAFC.
Area of sector
Area of ΔBAC
Area of the designed portion = 2 × (Area of segment AEC)
= 2 × (Area of sector BAEC − Area of ΔBAC)
Area of sector OCDE
Area of
Area of circle = πr2
Area of shaded region = Area of ΔOAB + Area of circle − Area of sector OCDE
Question 5:
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square.
Each quadrant is a sector of 90° in a circle of 1 cm radius.
Area of each quadrant
Area of circle = πr2 = π (1)2
Area of the shaded region = Area of square − Area of circle − 4 × Area of quadrant
Question 6:
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region).
Radius (r) of circle = 32 cm
AD is the median of
ABC.AD = 48 cm
In ΔABD,
AB2 = AD2 + BD2
Area of equilateral triangle,
Area of circle = πr2
Area of design = Area of circle − Area of ΔABC
Question 7:
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region.
Area of each of the 4 sectors is equal to each other and is a sector of 90° in a circle of 7 cm radius.
Area of each sector
Area of square ABCD = (Side)2 = (14)2 = 196 cm2
Area of shaded portion = Area of square ABCD − 4 × Area of each sector
Therefore, the area of shaded portion is 42 cm2.
Question 8:
Thegivenfigure depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
Distance around the track along its inner edge = AB + arc BEC + CD + arc DFA
Area of the track = (Area of GHIJ − Area of ABCD) + (Area of semi-circle HKI − Area of semi-circle BEC) + (Area of semi-circle GLJ − Area of semi-circle AFD)
Therefore, the area of the track is 4320 m2.
Question 9:
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Radius (r1) of larger circle = 7 cm
Radius (r2) of smaller circle
Area of semi-circle AECFB of larger circle
Area of the shaded region
= Area of smaller circle + Area of semi-circle AECFB − Area of ΔABC
Question 10:
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and]
Let the side of the equilateral triangle be a.
Area of equilateral triangle = 17320.5 cm2
Each sector is of measure 60°.
Area of sector ADEF
Area of shaded region = Area of equilateral triangle − 3 × Area of each sector
Question 11:
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the given figure). Find the area of the remaining portion of the handkerchief.
From the figure, it can be observed that the side of the square is 42 cm.
Area of square = (Side)2 = (42)2 = 1764 cm2
Area of each circle = πr2
Area of 9 circles = 9 × 154 = 1386 cm2
Area of the remaining portion of the handkerchief = 1764 − 1386 = 378 cm2
Question 12:
In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
(i) Since OACB is a quadrant, it will subtend 90° angle at O.
Area of quadrant OACB
(ii) Area of ΔOBD
Question 13:
In the given figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14]
In ΔOAB,
OB2 = OA2 + AB2
= (20)2 + (20)2
Radius (r) of circle
Area of OABC = (Side)2 = (20)2 = 400 cm2
Area of shaded region = Area of quadrant OPBQ − Area of OABC
= (628 − 400) cm2
= 228 cm2
Question 14:
Area of the shaded region = Area of sector OAEB − Area of sector OCFD
Question 15:
In ΔABC,
BC2 = AC2 + AB2
= (14)2 + (14)2
Radius (r1) of semi-circle drawn on
Area of sector
= 154 − (154 − 98)
= 98 cm2
Question 16:
Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each.
The designed area is the common region between two sectors BAEC and DAFC.
Area of sector
Area of ΔBAC
Area of the designed portion = 2 × (Area of segment AEC)
= 2 × (Area of sector BAEC − Area of ΔBAC)