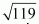Question 1:
How many tangents can a circle have?
A circle can have infinite tangents.
Question 2:
Fill in the blanks:
(i) A tangent to a circle intersects it in _______ point (s).
(ii) A line intersecting a circle in two points is called a __________.
(iii) A circle can have __________ parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ____.
(i) One
(ii) Secant
(iii) Two
(iv) Point of contact
(ii) Secant
(iii) Two
(iv) Point of contact
Question 3:
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm. (B) 13 cm (C) 8.5 cm (D)
cm
We know that the line drawn from the centre of the circle to the tangent is perpendicular to the tangent.
OP
PQ
By applying Pythagoras theorem in ΔOPQ,
OP2 + PQ2 = OQ2
52 + PQ2 =122
PQ2 =144 − 25
PQ =
cm.
Hence, the correct answer is (D).
It can be observed that AB and CD are two parallel lines. Line AB is intersecting the circle at exactly two points, P and Q. Therefore, line AB is the secant of this circle. Since line CD is intersecting the circle at exactly one point, R, line CD is the tangent to the circle.
OP
By applying Pythagoras theorem in ΔOPQ,
OP2 + PQ2 = OQ2
52 + PQ2 =122
PQ2 =144 − 25
PQ =
Hence, the correct answer is (D).
Question 4:
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
It can be observed that AB and CD are two parallel lines. Line AB is intersecting the circle at exactly two points, P and Q. Therefore, line AB is the secant of this circle. Since line CD is intersecting the circle at exactly one point, R, line CD is the tangent to the circle.